UpSetR charts

Venn diagrams blow.

Multiset Venn diagrams both blow and suck:

• Don’t make them; and

• Don’t make me interpret them; and

• Don’t try and put them in your presentations because you’ll get lost.

UpSetR provides a way to do the multi-set comparison thing without looking horrific.

We sample a few sets from the letters b-z:

library("UpSetR")

set.seed(1)

bucket_names <- paste0("set", 1:6)

buckets <- Map(
  function(x){
    bucket_size <- sample(1:25, 1)
    bucket <- sample(letters[-1], bucket_size, replace = FALSE)
    },
  bucket_names
  )

lapply(buckets, sort)

## $set1
## [1] "f" "k" "n" "o" "t" "v" "x"
## 
## $set2
##  [1] "c" "d" "f" "h" "i" "j" "k" "m" "n" "o" "q" "r" "s" "w" "y" "z"
## 
## $set3
##  [1] "b" "e" "i" "k" "l" "m" "p" "v" "x" "y"
## 
## $set4
##  [1] "b" "c" "d" "f" "g" "i" "k" "l" "n" "o" "p" "q" "s" "t" "u" "v" "w"
## [18] "x" "y" "z"
## 
## $set5
##  [1] "c" "f" "h" "j" "k" "n" "q" "r" "s" "t" "v" "w" "y"
## 
## $set6
##  [1] "b" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "p" "q" "r" "s" "t"
## [18] "u" "w" "x" "z"

The function upset takes a data-frame as input. But I’ve just defined my sets as a list of vectors. To convert these into a data-frame, use UpSetR::fromList:

fromList(buckets)

##    set1 set2 set3 set4 set5 set6
## 1     1    1    1    1    1    1
## 2     1    1    0    1    0    0
## 3     1    0    1    1    1    0
## 4     1    1    0    1    1    1
## 5     1    0    0    1    1    1
## 6     1    0    1    1    0    1
## 7     1    1    0    1    1    1
## 8     0    1    0    1    1    1
## 9     0    1    1    1    1    0
## 10    0    1    0    1    1    1
## 11    0    1    0    0    1    1
## 12    0    1    0    1    1    1
## 13    0    1    0    0    1    1
## 14    0    1    0    0    1    0
## 15    0    1    1    0    0    1
## 16    0    1    0    1    0    1
## 17    0    1    1    1    0    1
## 18    0    1    0    1    0    1
## 19    0    1    0    1    1    1
## 20    0    0    1    1    0    1
## 21    0    0    1    1    0    1
## 22    0    0    1    0    0    1
## 23    0    0    1    1    0    1
## 24    0    0    0    1    0    1
## 25    0    0    0    1    0    1

The letter ‘a’ is absent from every one of these sets. you could add a universe entry or an unobserved entry to the set-list passed to fromList if that’s what you’re into.

Otherwise, to generate an upset plot do the following:

upset(
  fromList(buckets)
  )

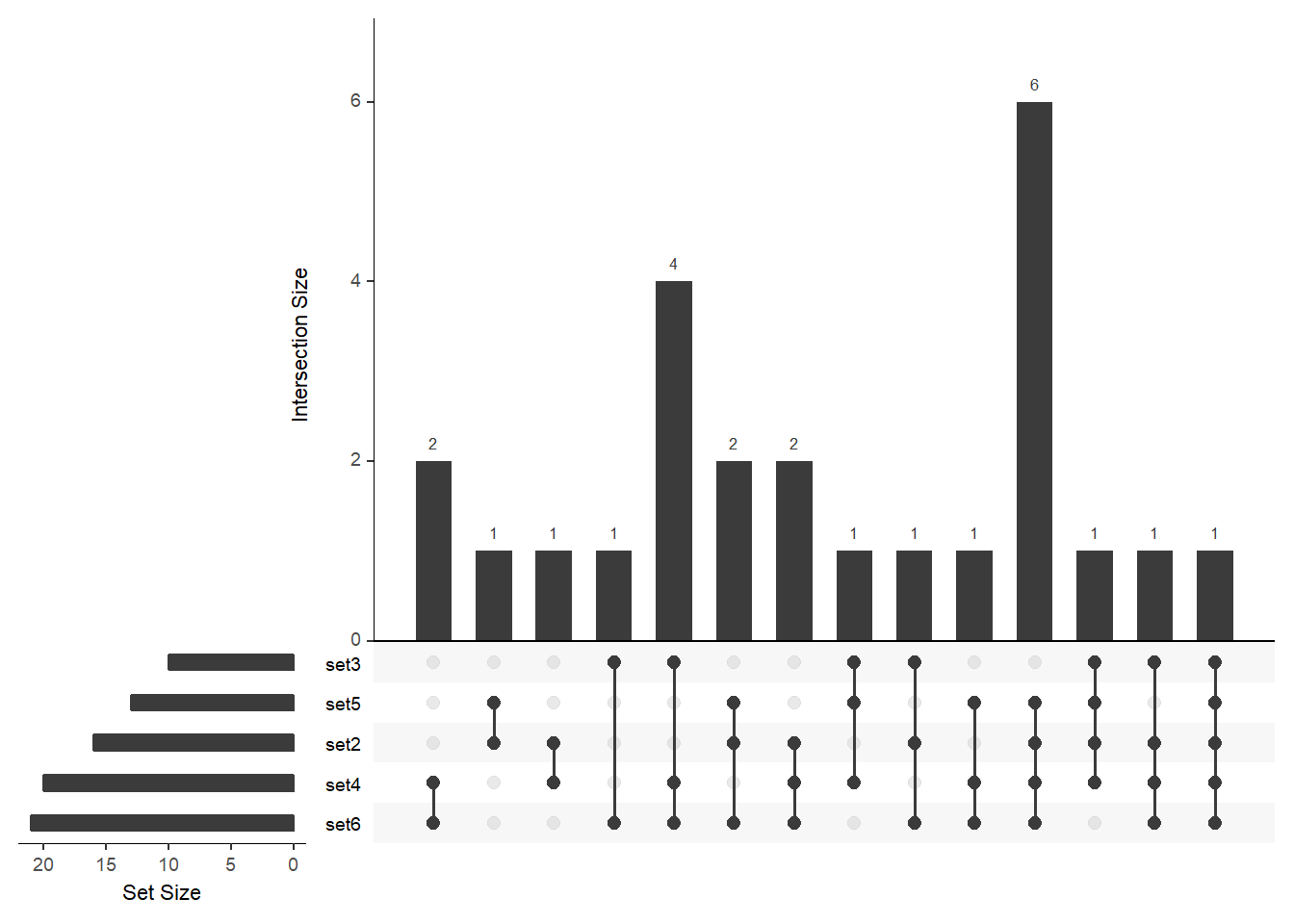
We note a couple of things:

• set1 is absent from the image, although it contained 7 elements;

• the elements of a given set are partitioned between the bars

  • eg, set3 contains 9 elements, that are split over the 4-5th, 8-9th and 12-14th columns (the numbers above these columns add up to 9) so each element in set3 is put into a single column that means, although the intersection between set3 and set6 is of size 8, there is only one element in the “set3 and set6” intersection column (the remaining 6 are partitioned across the other columns that contain both set3 and set6).

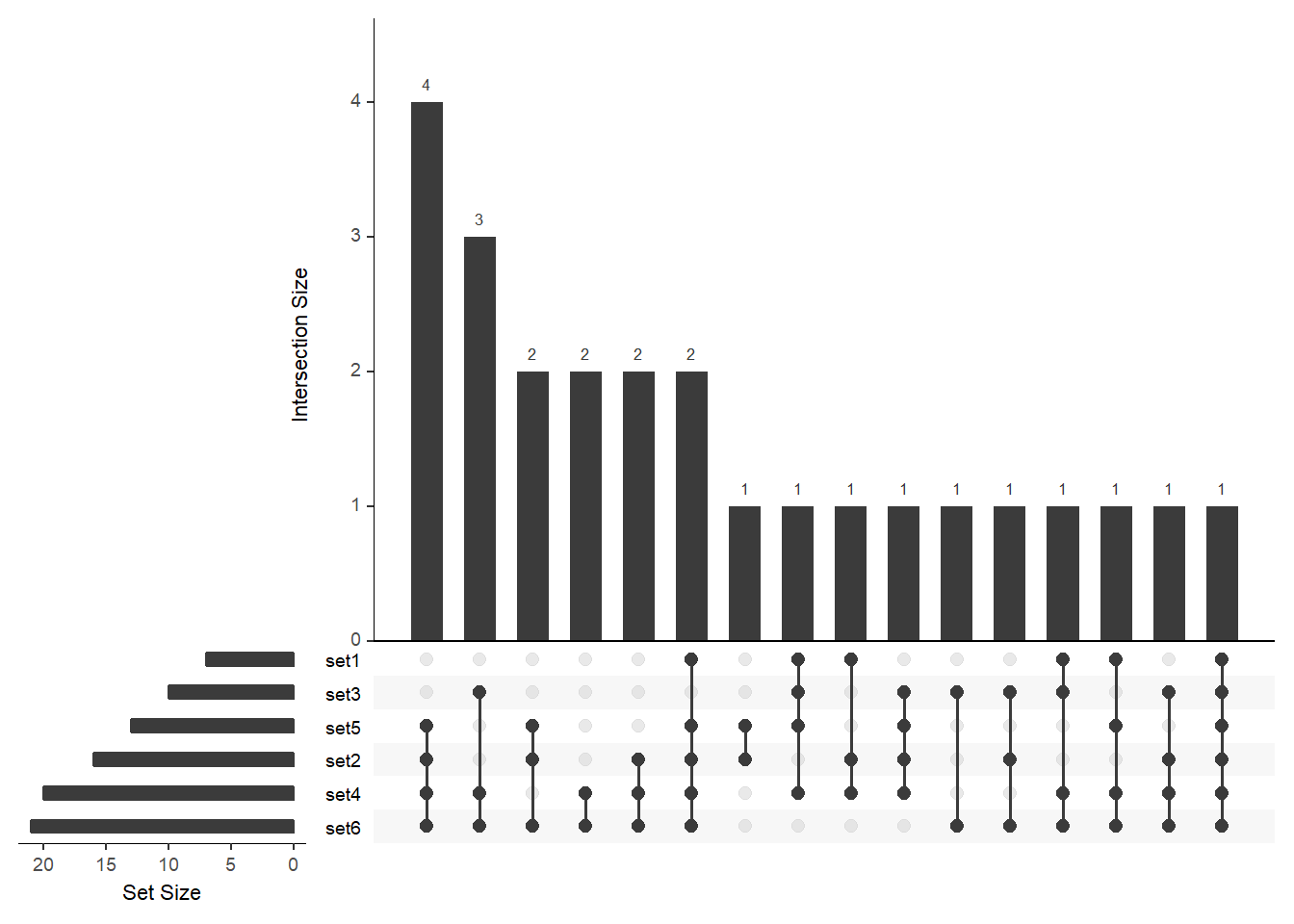
To ensure that all the sets are displayed in the figure, modify the nsets argument: You can order the bars by size (order.by = "freq") or by the number of sets that contributed to the intersection (order.by = "degree") or by both:

# order by freq
upset(
  fromList(buckets), nsets = length(buckets), order.by = "freq"
)

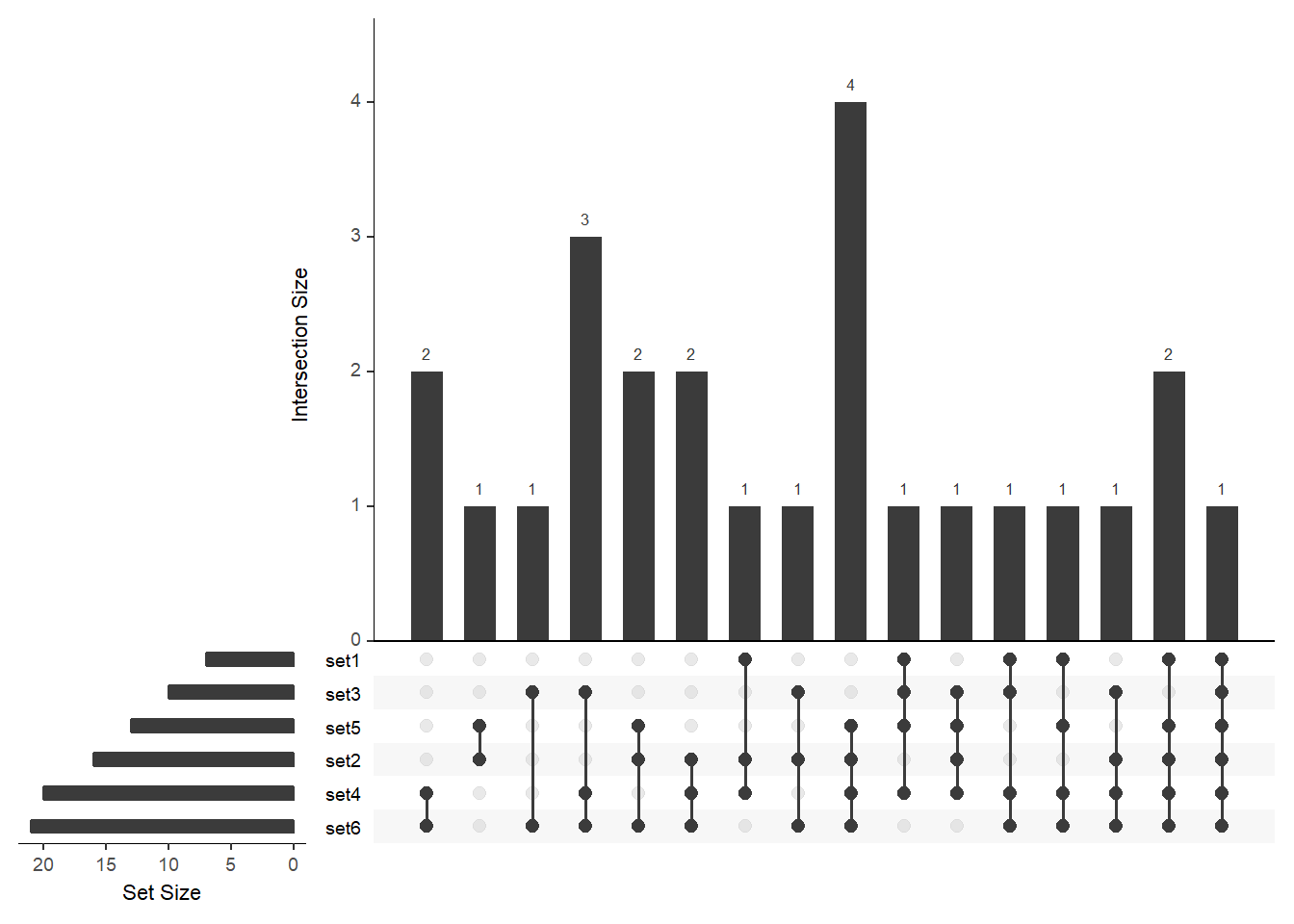
# order by degree and then by freq (not shown)
upset(
  fromList(buckets), order.by = c("freq", "degree"),
  nsets = length(buckets)
  )

# order by freq and then by degree
upset(
  fromList(buckets), order.by = c("degree", "freq"),
  nsets = length(buckets)
  )

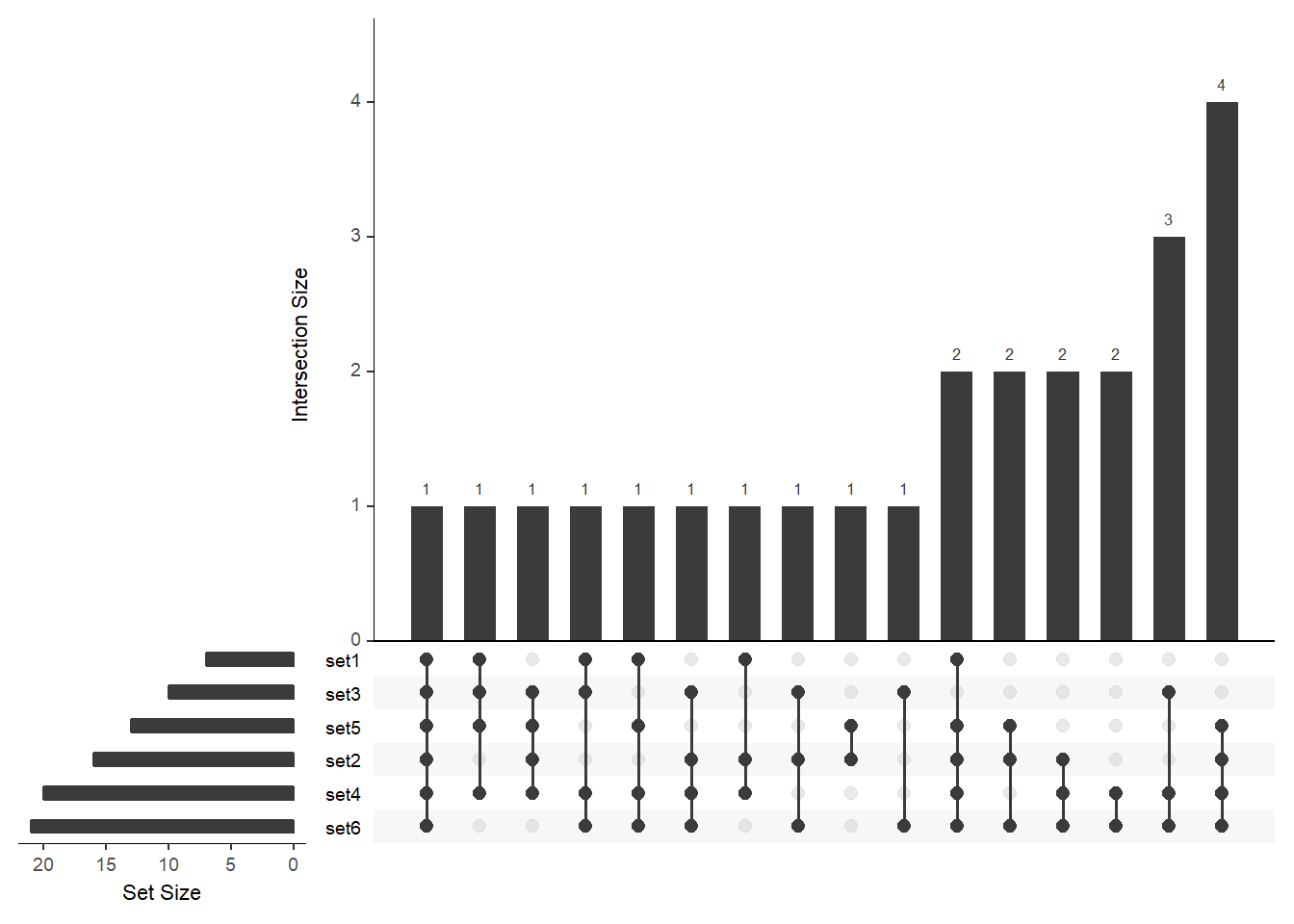
I found the latter a bit weird, in that order.by = c(“degree”, “freq”) sorts by increasing frequency, whereas order.by=“freq” sorts by decreasing frequency.